Solid modeling

Solid modeling (or modelling) is a consistent set of principles for mathematical and computer modeling of three-dimensional solids. Solid modeling is distinguished from related areas of geometric modeling and computer graphics by its emphasis on physical fidelity.^[1] Together, the principles of geometric and solid modeling form the foundation of computer-aided design and in general support the creation, exchange, visualization, animation, interrogation, and annotation of digital models of physical objects.

Contents 1 Overview 2 Mathematical foundations 3 Solid representation schemes 3.1 Parameterized primitive instancing 3.2 Spatial occupancy enumeration 3.3 Cell decomposition 3.4 Boundary representation 3.5 Constructive solid geometry 3.6 Sweeping 3.7 Implicit representation 3.8 Parametric and feature-based modeling 4 History of solid modelers 5 Computer-aided design 5.1 Entertainment 5.2 Medical solid modeling 5.3 Engineering 6 See also 7 References 8 External links

Overview

The use of solid modeling techniques allows for the automation of several difficult engineering calculations that are carried out as a part of the design process. Simulation, planning, and verification of processes such as machining and assembly were one of the main catalysts for the development of solid modeling. More recently, the range of supported manufacturing applications has been greatly expanded to include sheet metal manufacturing, injection molding, welding, pipe routing etc. Beyond traditional manufacturing, solid modeling techniques serve as the foundation for rapid prototyping, digital data archival and reverse engineering by reconstructing solids from sampled points on physical objects, mechanical analysis using finite elements, motion planning and NC path verification, kinematic and dynamic analysis of mechanisms, and so on. A central problem in all these applications is the ability to effectively represent and manipulate three-dimensional geometry in a fashion that is consistent with the physical behavior of real artifacts. Solid modeling research and development has effectively addressed many of these issues, and continues to be a central focus of computer-aided engineering.

Mathematical foundations

The notion of solid modeling as practiced today relies on the specific need for informational completeness in mechanical geometric modeling systems, in the sense that any computer model should support all geometric queries that may be asked of its corresponding physical object. The requirement implicitly recognizes the possibility of several computer representations of the same physical object as long as any two such representations are consistent. It is impossible to computationally verify informational completeness of a representation unless the notion of a physical object is defined in terms of computable mathematical properties and independent of any particular representation. Such reasoning led to the development of the modeling paradigm that has shaped the field of solid modeling as we know it today.^[2]

All manufactured components have finite size and well behaved boundaries, so initially the focus was on mathematically modeling rigid parts made of homogeneous isotropic material that could be added or removed. These postulated properties can be translated into properties of subsets of three-dimensional Euclidean space. The two common approaches to define solidity rely on point-set topology and algebraic topology respectively. Both models specify how solids can be built from simple pieces or cells.

According to the continuum point-set model of solidity, all the points of any X ⊂ ℝ³ can be classified according to their neighborhoods with respect to X as interior, exterior, or boundary points. Assuming ℝ³ is endowed with the typical Euclidean metric, a neighborhood of a point p ∈X takes the form of an open ball. For X to be considered solid, every neighborhood of any p ∈X must be consistently three dimensional; points with lower dimensional neighborhoods indicate a lack of solidity. Dimensional homogeneity of neighborhoods is guaranteed for the class of closed regular sets, defined as sets equal to the closure of their interior. Any X ⊂ ℝ³ can be turned into a closed regular set or regularized by taking the closure of its interior, and thus the modeling space of solids is mathematically defined to be the space of closed regular subsets of ℝ³ (by the Heine-Borel theorem it is implied that all solids are compact sets). In addition, solids are required to be closed under the Boolean operations of set union, intersection, and difference (to guarantee solidity after material addition and removal). Applying the standard Boolean operations to closed regular sets may not produce a closed regular set, but this problem can be solved by regularizing the result of applying the standard Boolean operations.^[3] The regularized set operations are denoted ∪^∗, ∩^∗, and −^∗.

The combinatorial characterization of a set X ⊂ ℝ³ as a solid involves representing X as an orientable cell complex so that the cells provide finite spatial addresses for points in an otherwise innumerable continuum.^[1] The class of semi-analytic bounded subsets of Euclidean space is closed under Boolean operations (standard and regularized) and exhibits the additional property that every semi-analytic set can be stratified into a collection of disjoint cells of dimensions 0,1,2,3. A triangulation of a semi-analytic set into a collection of points, line segments, triangular faces, and tetrahedral elements is an example of a stratification that is commonly used. The combinatorial model of solidity is then summarized by saying that in addition to being semi-analytic bounded subsets, solids are three-dimensional topological polyhedra, specifically three-dimensional orientable manifolds with boundary.^[4] In particular this implies the Euler characteristic of the combinatorial boundary^[5] of the polyhedron is 2. The combinatorial manifold model of solidity also guarantees the boundary of a solid separates space into exactly two components as a consequence of the Jordan-Brouwer theorem, thus eliminating sets with non-manifold neighborhoods that are deemed impossible to manufacture.

The point-set and combinatorial models of solids are entirely consistent with each other, can be used interchangeably, relying on continuum or combinatorial properties as needed, and can be extended to n dimensions. The key property that facilitates this consistency is that the class of closed regular subsets of ℝⁿ coincides precisely with homogeneously n-dimensional topological polyhedra. Therefore every n-dimensional solid may be unambiguously represented by its boundary and the boundary has the combinatorial structure of an n−1-dimensional polyhedron having homogeneously n−1-dimensional neighborhoods.

Solid representation schemes

Based on assumed mathematical properties, any scheme of representing solids is a method for capturing information about the class of semi-analytic subsets of Euclidean space. This means all representations are different ways of organizing the same geometric and topological data in the form of a data structure. All representation schemes are organized in terms of a finite number of operations on a set of primitives. Therefore the modeling space of any particular representation is finite, and any single representation scheme may not completely suffice to represent all types of solids. For example, solids defined via combinations of regularized boolean operations cannot necessarily be represented as the sweep of a primitive moving according to a space trajectory, except in very simple cases. This forces modern geometric modeling systems to maintain several representation schemes of solids and also facilitate efficient conversion between representation schemes.

Below is a list of common techniques used to create or represent solid models.^[4] Modern modeling software may use a combination of these schemes to represent a solid.

Parameterized primitive instancing

This scheme is based on the notion of families of objects, each member of a family distinguishable from the other by a few parameters. Each object family is called a generic primitive, and individual objects within a family are called primitive instances. For example a family of bolts is a generic primitive, and a single bolt specified by a particular set of parameters is a primitive instance. The distinguishing characteristic of pure parameterized instancing schemes is the lack of means for combining instances to create new structures which represent new and more complex objects. The other main drawback of this scheme is the difficulty of writing algorithms for computing properties of represented solids. A considerable amount of family-specific information must be built into the algorithms and therefore each generic primitive must be treated as a special case, allowing no uniform overall treatment.

Spatial occupancy enumeration

This scheme is essentially a list of spatial cells occupied by the solid. The cells, also called voxels are cubes of a fixed size and are arranged in a fixed spatial grid (other polyhedral arrangements are also possible but cubes are the simplest). Each cell may be represented by the coordinates of a single point, such as the cell's centroid. Usually a specific scanning order is imposed and the corresponding ordered set of coordinates is called a spatial array. Spatial arrays are unambiguous and unique solid representations but are too verbose for use as 'master' or definitional representations. They can, however, represent coarse approximations of parts and can be used to improve the performance of geometric algorithms, especially when used in conjunction with other representations such as constructive solid geometry.

Cell decomposition

This scheme follows from the combinatoric (algebraic topological) descriptions of solids detailed above. A solid can be represented by its decomposition into several cells. Spatial occupancy enumeration schemes are a particular case of cell decompositions where all the cells are cubical and lie in a regular grid. Cell decompositions provide convenient ways for computing certain topological properties of solids such as its connectedness (number of pieces) and genus (number of holes). Cell decompositions in the form of triangulations are the representations used in 3d finite elements for the numerical solution of partial differential equations. Other cell decompositions such as a Whitney regular stratification or Morse decompositions may be used for applications in robot motion planning.^[6]

Boundary representation

In this scheme a solid is represented by the cellular decomposition of its boundary. Since the boundaries of solids have the distinguishing property that they separate space into regions defined by the interior of the solid and the complementary exterior according to the Jordan-Brouwer theorem discussed above, every point in space can unambiguously be tested against the solid by testing the point against the boundary of the solid. Recall that ability to test every point in the solid provides a guarantee of solidity. Using ray casting it is possible to count the number of intersections of a cast ray against the boundary of the solid. Even number of intersections correspond to exterior points, and odd number of intersections correspond to interior points. The assumption of boundaries as manifold cell complexes forces any boundary representation to obey disjointedness of distinct primitives, i.e. there are no self-intersections that cause non-manifold points. In particular, the manifoldness condition implies all pairs of vertices are disjoint, pairs of edges are either disjoint or intersect at one vertex, and pairs of faces are disjoint or intersect at a common edge. Several data structures that are combinatorial maps have been developed to store boundary representations of solids. In addition to planar faces, modern systems provide the ability to store quadrics and NURBS surfaces as a part of the boundary representation. Boundary representations have evolved into a ubiquitous representation scheme of solids in most commercial geometric modelers because of their flexibility in representing solids exhibiting a high level of geometric complexity.

Constructive solid geometry

Constructive solid geometry (CSG) connotes a family of schemes for representing rigid solids as Boolean constructions or combinations of primitives via the regularized set operations discussed above. CSG and boundary representations are currently the most important representation schemes for solids. CSG representations take the form of ordered binary trees where non-terminal nodes represent either rigid transformations (orientation preserving isometries) or regularized set operations. Terminal nodes are primitive leaves that represent closed regular sets. The semantics of CSG representations is clear. Each subtree represents a set resulting from applying the indicated transformations/regularized set operations on the set represented by the primitive leaves of the subtree. CSG representations are particularly useful for capturing design intent in the form of features corresponding to material addition or removal (bosses, holes, pockets etc). The attractive properties of CSG include conciseness, guaranteed validity of solids, computationally convenient Boolean algebraic properties, and natural control of a solid's shape in terms of high level parameters defining the solid's primitives and their positions and orientations. The relatively simple data structure and elegant recursive algorithms have further contributed to the popularity of CSG.

Sweeping

The basic notion embodied in sweeping schemes is simple. A set moving through space may trace or sweep out volume (a solid) that may be represented by the moving set and its trajectory. Such a representation is important in the context of applications such as detecting the material removed from a cutter as it moves along a specified trajectory, computing dynamic interference of two solids undergoing relative motion, motion planning, and even in computer graphics applications such as tracing the motions of a brush moved on a canvas. Most commercial CAD systems provide (limited) functionality for constructing swept solids mostly in the form of a two dimensional cross section moving on a space trajectory transversal to the section. However, current research has shown several approximations of three dimensional shapes moving across one parameter, and even multi-parameter motions.

Implicit representation

A very general method of defining a set of points X is to specify a predicate that can be evaluated at any point in space. In other words, X is defined implicitly to consist of all the points that satisfy the condition specified by the predicate. The simplest form of a predicate is the condition on the sign of a real valued function resulting in the familiar representation of sets by equalities and inequalities. For example if 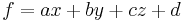the conditions 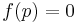,,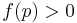 and 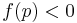represent respectively a plane and two open linear halfspaces. More complex functional primitives may be defined by boolean combinations of simpler predicates. Furthermore, the theory of R-functions allow conversions of such representations into a single function inequality for any closed semi analytic set. Such a representation can be converted to a boundary representation using polygonization algorithms, for example, the marching cubes algorithm.

Parametric and feature-based modeling

Features are defined to be parametric shapes associated with attributes such as intrinsic geometric parameters (length, width, depth etc), position and orientation, geometric tolerances, material properties, and references to other features.^[7] Features also provide access to related production processes and resource models. Thus, features have a semantically higher level than primitive closed regular sets. Features are generally expected to form a basis for linking CAD with downstream manufacturing applications, and also for organizing databases for design data reuse.

History of solid modelers

The historical development of solid modelers has to be seen in context of the whole history of CAD, the key milestones being the development of the research system BUILD followed by its commercial spin-off Romulus which went on to influence the development of Parasolid, ACIS and Solid Modeling Solutions. Other contributions came from Mäntylä, with his GWB and from the GPM project which contributed, among other things, hybrid modeling techniques at the beginning of the 1980s.

Computer-aided design

Solid modelers have become commonplace in engineering departments in the last ten years due to faster computers and competitive software pricing. Solid modeling software creates a virtual 3D representation of components for machine design and analysis.^[8] A typical graphical user interface includes programmable macros, keyboard shortcuts and dynamic model manipulation. The ability to dynamically re-orient the model, in real-time shaded 3-D, is emphasized and helps the designer maintain a mental 3-D image.

A solid part model generally consists of a group of features, added one at a time, until the model is complete. Engineering solid models are built mostly with sketcher-based features; 2-D sketches that are swept along a path to become 3-D. These may be cuts, or extrusions for example.

Design work on components is usually done within the context of the whole product using assembly modeling methods. An assembly model incorporates references to individual part models that comprise the product.^[9]

Another type of modeling technique is 'surfacing' (Freeform surface modeling). Here, surfaces are defined, trimmed and merged, and filled to make solid. The surfaces are usually defined with datum curves in space and a variety of complex commands. Surfacing is more difficult, but better applicable to some manufacturing techniques, like injection molding. Solid models for injection molded parts usually have both surfacing and sketcher based features.

Engineering drawings are created semi-automatically and reference the solid models.

The learning curve for these software packages is steep, but a fluent machine designer who can master these software packages is highly productive.

The modeling of solids is only the minimum requirement of a CAD system’s capabilities.

Parametric modeling uses parameters to define a model (dimensions, for example). The parameter may be modified later, and the model will update to reflect the modification. Typically, there is a relationship between parts, assemblies, and drawings. A part consists of multiple features, and an assembly consists of multiple parts. Drawings can be made from either parts or assemblies.

Example: A shaft is created by extruding a circle 100 mm. A hub is assembled to the end of the shaft. Later, the shaft is modified to be 200 mm long (click on the shaft, select the length dimension, modify to 200). When the model is updated the shaft will be 200 mm long, the hub will relocate to the end of the shaft to which it was assembled, and the engineering drawings and mass properties will reflect all changes automatically.

Examples of parameters are: dimensions used to create model features, material density, formulas to describe swept features, imported data (that describe a reference surface, for example).

Related to parameters, but slightly different are Constraints. Constraints are relationships between entities that make up a particular shape. For a window, the sides might be defined as being parallel, and of the same length.

Parametric modeling is obvious and intuitive. But for the first three decades of CAD this was not the case. Modification meant re-draw, or add a new cut or protrusion on top of old ones. Dimensions on engineering drawings were created, instead of shown.

Parametric modeling is very powerful, but requires more skill in model creation. A complicated model for an injection molded part may have a thousand features, and modifying an early feature may cause later features to fail. Skillfully created parametric models are easier to maintain and modify.

Parametric modeling also lends itself to data re-use. A whole family of capscrews can be contained in one model, for example.

Entertainment

Animation of computer generated characters is, technically, an example of parametric modeling, though few in the industry would consider it to be. Characters' skin is modeled with NURBS patches and stitched together or polygon modeled. The skin of characters is then parametrically associated to a skeleton within characters (with many characters' skins now being driven by muscle simulation systems). The skeleton of a character is rotated into poses, which parametrically drives the shape of the characters' skin for each frame to create animation.

Medical solid modeling

Modern computed axial tomography and magnetic resonance imaging scanners can be used to create solid models of internal body features, so-called volume rendering. Optical 3D scanners can be used to create point clouds or polygon mesh models of external body features.

Uses of medical solid modeling;

• Visualization
• Visualization of specific body tissues (just blood vessels and tumor, for example)
• Designing prosthetics, orthotics, and other medical and dental devices (this is sometimes called mass customization)
• Creating polygon mesh models for rapid prototyping (to aid surgeons preparing for difficult surgeries, for example)
• Combining polygon mesh models with CAD solid modeling (design of hip replacement parts, for example)
• Computational analysis of complex biological processes, e.g. air flow, blood flow
• Computational simulation of new medical devices and implants in vivo

If the use goes beyond visualization of the scan data, processes like image segmentation and image-based meshing will be necessary to generate an accurate and realistic geometrical description of the scan data.

Engineering

Because CAD programs running on computers “understand” the true geometry comprising complex shapes, many attributes of for a 3‑D solid, such as its center of gravity, volume, and mass, can be quickly calculated. For instance, the cube shown at the top of this article measures 8.4 mm from flat to flat. Despite its many radii and the shallow pyramid on each of its six faces, its properties are readily calculated for the designer, as shown in in the screenshot at right.

See also

• Computer graphics
• Computational geometry
• Euler boundary representation
• Engineering drawing
• Technical drawing
• List of CAD companies

References

External links

• sgCore C++/C# library
• Example of relational solid modeling
• The Solid Modeling Association
• resources for learning Solid Modeling